Sombrero vs. Volleyball: Difference between revisions
imported>Greycat No edit summary |
imported>Erathaol Noting that the formula is incorrect. |
||
| (10 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{ | {{rewrite|The section on Wild Hares needs to be updated. The Bandersnatch examples need to be re-written. The ML Stat formula is also incorrect (ML/3 not ML/4) meaning the math needs to be redone }} | ||
__NOTOC__ | __NOTOC__ | ||
The two most popular stat-gain familiars can be pigeonholed into two categories: volleyballs and sombreros. For an analysis of the best familiar equipment for stat gains while using such familiars, see the [[Blood-Faced Volleyball]] and [[Hovering Sombrero]] articles. The present page is concerned with comparing volleyballs against sombreros. | The two most popular stat-gain familiars can be pigeonholed into two categories: volleyballs and sombreros. For an analysis of the best familiar equipment for stat gains while using such familiars, see the [[Blood-Faced Volleyball]] and [[Hovering Sombrero]] articles. The present page is concerned with comparing volleyballs against sombreros. The main takeaway is that deciding which familiar to use is dependent on [[Monster Level]]. | ||
==Sombrero vs. Volleyball Formula== | |||
In the formulas below, VW is volleyball weight, SW is sombrero weight, and ML is monster level. | In the formulas below, VW is volleyball weight, SW is sombrero weight, and ML is monster level. | ||
The formula for extra stats given by the Hovering Sombrero of weight SW is: | |||
<center>stats = | <center>stats = (ML/4)*(0.1 + 0.005*SW)</center> | ||
<center>(The Sombrero grants 10% of the stats you receive normally, plus an additional 0.5% per pound of Sombrero)</center> | |||
And for the Blood-faced Volleyball: | And for the Blood-faced Volleyball: | ||
<center>stats = | <center>stats = 2 + VW/5</center> | ||
To find the point where the sombrero matches the volleyball, we must solve for monster level in terms of the two weights. Thus, we start with: | To find the point where the sombrero matches the volleyball, we must solve for monster level in terms of the two weights. Thus, we start with: | ||
<center> | <center>2 + VW/5 = (ML/4) * (0.1 + 0.005*SW)</center> | ||
However, given that we have obtained both (or neither) familiar equipment, as well as assuming that any equipment/buffs we want can be switched between them (e.g., [[wax lips]], [[Leash of Linguini (skill)|Leash of Linguini]]), we can say that: | However, given that we have obtained both (or neither) familiar equipment, as well as assuming that any equipment/buffs we want can be switched between them (e.g., [[wax lips]], [[Leash of Linguini (skill)|Leash of Linguini]]), we can say that: | ||
<center> | <center>VW = SW</center> | ||
Setting that value equal to W, we substitute: | Setting that value equal to W, we substitute: | ||
<center>W = | <center>2 + W/5 = (ML/4) * (0.1 + 0.005 * W)</center> | ||
divide through by (0.1 + 0.005*W) to get: | |||
<center>(2 + W/5) / (0.1 + 0.005 * W) = ML/4</center> | |||
Re-arranging and multiplying through by 4, we get: | |||
<center>ML = 4 * (2 + W/5) / (0.1 + 0.005*W)</center> | |||
===Interpretation=== | |||
This cannot be simplified any more until either a weight (W) or Monster Level (ML) are provided. The below chart showing break-even points plots this formula graphically. | |||
< | It should be noted that with equally weighted familiars, a Sombrero will always be better than a Volleyball ''at 160 or more Monster Level.'' This is because the limit as W approaches infinity of the ML formula above is 160. | ||
* According to Wolfram Alpha, <pre>limit (4 * (2 + W/5) / (0.1 + 0.005*W)) as W->infinity</pre> = [http://www.wolframalpha.com/input/?i=limit+%284+*+%282+%2B+W%2F5%29+%2F+%280.1+%2B+0.005*W%29%29+as+W-%3Einfinity 160 Monster Level]. | |||
Solving the formula for 1 pound familiars, it can also be noted that with equally weighted familiars, ''at 83 or less Monster Level,'' a Volleyball is always better than a Sombrero. | |||
== | == Charts == | ||
* Comparing different weight Sombreros and Volleyballs is much more useful than comparing equal weight ones, but figuring out where to stop using one familiar and start using another can be tricky. The following graph attempts to make that process easier by giving a visualization of the familiars at various weights and Monster Levels, showing how many stats they give. | |||
* [[Image:bugbear_vs_sombrero_may_2014_update_thumb.png|link=http://ben.bloomroad.com/kol/bugbear_vs_sombrero_may_2014_update.png|Baby Bugged Bugbear (wearing a balaclava) vs Volleyball vs Sombrero]] | |||
* The Sombrero's stat cap will always be higher as compared to an equivalent weight volleyball (or baby bugged bugbear wearing a balaclava). The following graph shows those break-even Monster Levels, and how many stats you'd get from the Sombrero (or Volleyball/Bugbear) at the break-even point of ML for each weight. | |||
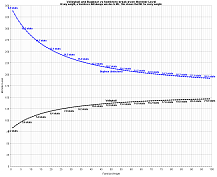
*[[Image:bugbear_vs_sombrero_breakeven_thumb.png|link=http://ben.bloomroad.com/kol/bugbear_vs_sombrero_breakeven.png|Breakeven ML for Volleyball (and Bugbear) vs. Sombrero]] | |||
*[http://ben.bloomroad.com/kol/ | |||
* | |||
*[[Image: | |||
==Examples== | ==Examples== | ||
Example: Picking a weight such as 20 pounds gives: ML = 4*(2+20/5) / (0.1 + 0.005*20) = 4*(6) / (0.2) = 120. So when both the Volleyball and Sombrero are 20 pounds: ''if you are fighting monsters more than 120 ML'', use the '''sombrero'''; and ''less than 120 ML'', use the '''volleyball'''. | |||
==Why does a Sombrero always win at ''some'' monster level?== | |||
Because the Sombrero's stat bonuses grow with monster level, and the volleyball's does not. | |||
Computer scientists define the growth of a function using [[Wikipedia:Big O notation|Big O notation]], which describes the behavior of a function as its argument gets arbitrarily large. In the case of the stat gains for volleyballs and sombreros, volleyball stat gains are constant at a given volleyball weight. They are ''O''(''v'') = ''O''(''C'') = ''O''(''1''). However, the sombrero formula contains a non-constant factor in its numerator, the monster level, so its stat gains are ''O''(''m''), where ''m'' is the monster level. Since sombrero stat gains always grow as ''m'' increases and volleyball stat gains are independent of ''m'', with a large enough ''m'', the sombrero will always outperform the volleyball. This ignores the fact that the sombrero has a stat cap, because in order to reach the current stat cap of 230, a volleyball would need to weigh 230 = 2 + w/5 => w = 228*5 = 1140 pounds, which is unrealistic. | |||
Under extreme conditions, the [[Wild Hare|Wild Hare]]'s ability to provide extra rollover adventures will provide more (net) substats per adventure than either the volleyball or the sombrero because the benefit from the Wild Hare is ''O''(''m''). Since this requires an infinite supply of level 9200+ monsters, it's really only feasible for high-stat characters fighting against scaling monsters such as the [[Sloppy Seconds Diner]] (cap at 11,111 ml), [[Fernswarthy's Basement]] and [[Special Monsters|Crimbo monsters]]. | |||
[[Category:Familiars| Sombrero vs Volleyball]] | [[Category:Familiars| Sombrero vs Volleyball]] | ||
[[Category:Game Mechanics]] | [[Category:Game Mechanics]] | ||
Latest revision as of 02:34, 3 November 2022

|
The Hermit humbly requests that this page be rewritten or expanded.
|
The two most popular stat-gain familiars can be pigeonholed into two categories: volleyballs and sombreros. For an analysis of the best familiar equipment for stat gains while using such familiars, see the Blood-Faced Volleyball and Hovering Sombrero articles. The present page is concerned with comparing volleyballs against sombreros. The main takeaway is that deciding which familiar to use is dependent on Monster Level.
Sombrero vs. Volleyball Formula
In the formulas below, VW is volleyball weight, SW is sombrero weight, and ML is monster level.
The formula for extra stats given by the Hovering Sombrero of weight SW is:
And for the Blood-faced Volleyball:
To find the point where the sombrero matches the volleyball, we must solve for monster level in terms of the two weights. Thus, we start with:
However, given that we have obtained both (or neither) familiar equipment, as well as assuming that any equipment/buffs we want can be switched between them (e.g., wax lips, Leash of Linguini), we can say that:
Setting that value equal to W, we substitute:
divide through by (0.1 + 0.005*W) to get:
Re-arranging and multiplying through by 4, we get:
Interpretation
This cannot be simplified any more until either a weight (W) or Monster Level (ML) are provided. The below chart showing break-even points plots this formula graphically.
It should be noted that with equally weighted familiars, a Sombrero will always be better than a Volleyball at 160 or more Monster Level. This is because the limit as W approaches infinity of the ML formula above is 160.
- According to Wolfram Alpha,
limit (4 * (2 + W/5) / (0.1 + 0.005*W)) as W->infinity
= 160 Monster Level.
Solving the formula for 1 pound familiars, it can also be noted that with equally weighted familiars, at 83 or less Monster Level, a Volleyball is always better than a Sombrero.
Charts
- Comparing different weight Sombreros and Volleyballs is much more useful than comparing equal weight ones, but figuring out where to stop using one familiar and start using another can be tricky. The following graph attempts to make that process easier by giving a visualization of the familiars at various weights and Monster Levels, showing how many stats they give.

- The Sombrero's stat cap will always be higher as compared to an equivalent weight volleyball (or baby bugged bugbear wearing a balaclava). The following graph shows those break-even Monster Levels, and how many stats you'd get from the Sombrero (or Volleyball/Bugbear) at the break-even point of ML for each weight.
Examples
Example: Picking a weight such as 20 pounds gives: ML = 4*(2+20/5) / (0.1 + 0.005*20) = 4*(6) / (0.2) = 120. So when both the Volleyball and Sombrero are 20 pounds: if you are fighting monsters more than 120 ML, use the sombrero; and less than 120 ML, use the volleyball.
Why does a Sombrero always win at some monster level?
Because the Sombrero's stat bonuses grow with monster level, and the volleyball's does not.
Computer scientists define the growth of a function using Big O notation, which describes the behavior of a function as its argument gets arbitrarily large. In the case of the stat gains for volleyballs and sombreros, volleyball stat gains are constant at a given volleyball weight. They are O(v) = O(C) = O(1). However, the sombrero formula contains a non-constant factor in its numerator, the monster level, so its stat gains are O(m), where m is the monster level. Since sombrero stat gains always grow as m increases and volleyball stat gains are independent of m, with a large enough m, the sombrero will always outperform the volleyball. This ignores the fact that the sombrero has a stat cap, because in order to reach the current stat cap of 230, a volleyball would need to weigh 230 = 2 + w/5 => w = 228*5 = 1140 pounds, which is unrealistic.
Under extreme conditions, the Wild Hare's ability to provide extra rollover adventures will provide more (net) substats per adventure than either the volleyball or the sombrero because the benefit from the Wild Hare is O(m). Since this requires an infinite supply of level 9200+ monsters, it's really only feasible for high-stat characters fighting against scaling monsters such as the Sloppy Seconds Diner (cap at 11,111 ml), Fernswarthy's Basement and Crimbo monsters.
